Even vs uneven spacing#
Evenly spaced data#
As long as this data is evenly spaced with step size \(h\), we can use finite difference directly.
BUT: Be aware of the boundaries! The central difference is the superior choice for the interior points, but you will need forward and backward differences at the boundaries.
Example: Find the derivative of a discretized function#
Say we have data for a function \(y(x)\) that looks like a parabola. We measured it every \(h\) steps in the range [a,b], so we have data for \(x_0 = a\) to \(x_n = b\)
x = np.array([0,1,2,3,4,5,6,7,8,9])
y = np.array([0.5, 1.48765432, 2.22839506, 2.72222222, 2.9691358, 2.9691358,
2.72222222, 2.22839506, 1.48765432, 0.5 ])
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('y vs x')
plt.show()
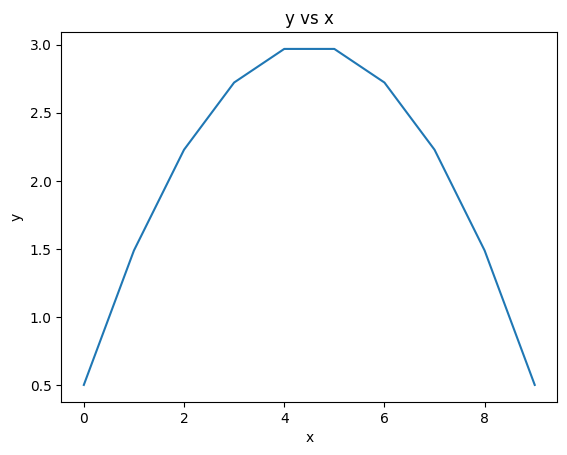
If we just applied central difference to this function would encounter problems at the endpoints.
The numpy function gradient identifies the endpoints and treats them with forward / backward difference:
dy = np.gradient(y,x)
plt.plot(x, dy)
plt.xlabel('x')
plt.ylabel('dy')
plt.title('dy vs x')
plt.show()
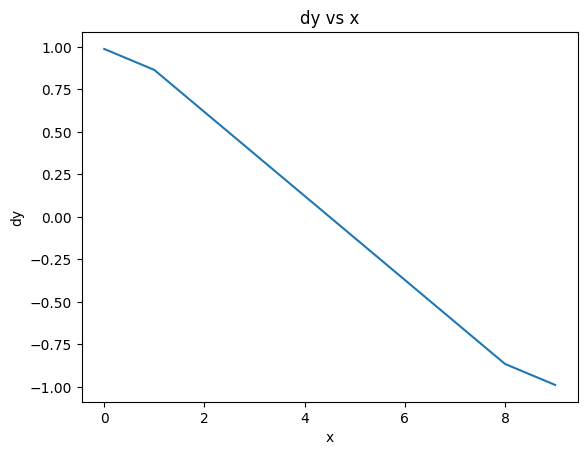
This looks good in the middle but the ends are funny…
What do you think?
dy2 = np.gradient(y,x, edge_order = 2)
plt.plot(x, dy)
plt.plot(x, dy2)
plt.xlabel('x')
plt.ylabel('dy')
plt.title('dy vs x')
plt.show()
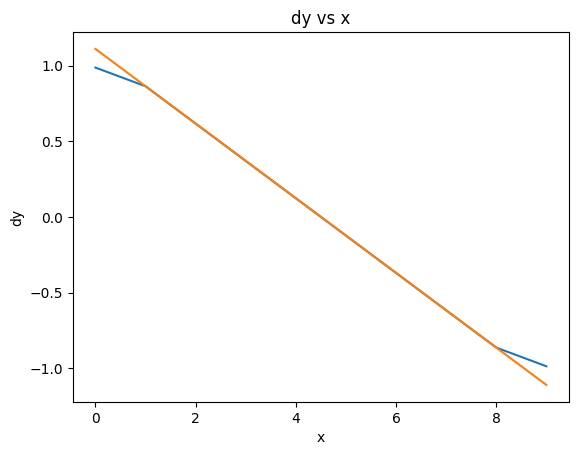
Bingo! Using the higher order edge cases solved the problem!
Note, this is the foundation of the finite difference method for solving differential equations.
Unevenly spaced data#
When data is unevenly spaced we can always do first-order forward / backward difference. If we want higher order generally have to resort to a local polynomial fitting.
Recall the cubic Lagrange interpolation. We can take the (analytic) derivative and find:
which is of comparable accuracy to the centeral difference and recovers it if the points are equally spaced.


