Quantifying error

Quantifying error#

True Absolute Error#

The difference between the true answer and an approximate answer is called the True Absolute Error:

\(E_t = |True - Approx| \)

Only really useful when the true value is known.

Example: What is the derivative of \(sin(x)\) at \(x=0\)?#

Recall: \(\frac{d sin (x)}{dx} = lim_{\Delta x->0} \frac{sin(x+\Delta x)-sin(x)}{\Delta x}\)

True: \(\frac{d sin (x)}{dx} = cos(x)\)

from numpy import cos, sin, abs
value_true = cos(0)
print(value_true) 

1.0

Define a function (for later use) approx which takes a parameter, \(\Delta x\):

\(approx(\Delta x) = \frac{sin(x+\Delta x)-sin(x)}{\Delta x}\)

def approx(delta_x):
    return (sin(0+delta_x)-sin(0))/delta_x

For \(\Delta x = .1\),

value_approx = approx(delta_x = .1)
print(value_approx)

0.9983341664682815

The true absolute error is therefore,

E_t = abs(value_true - value_approx)
print(E_t)

0.0016658335317184525

True relative error#

Often the absolute error is not so useful since it doesn’t consider the magnitude of the value.

E.g. GPS has an error of about ~1m. Is that important for calculating distance for a long road trip? What about a self-driving the car?

Also note that absolute error has units which complicates generalization.

The true relative error is defined as,

\(\epsilon_t = \frac{E_t}{True}\)

or as a percent,

\(\frac{E_t}{True} \times 100 \%\)

Example: What is the relative error from the previous calculation?#

eps_t = E_t/value_true
print(eps_t)

0.0016658335317184525

Approximate absolute and relative error#

What if we don’t have the true value?

Numerical methods typically have a tunable parameter that controls accuracy (viz. \(\Delta x\) above). We can estimate the error for sequential approximations, using the better approximation in place of the True one.

\(E_a = |Better\ approx - approx|\)

\(\epsilon_a = \frac{E_a}{Better\ approx}\)

Example: Use smaller step sizes to find the approximate error and fracitonal error.#

E_a = abs(approx(.01) - approx(.1))
print(E_a)

0.0016491669483849059

epsilon_a = E_a/approx(.01)
print(epsilon_a)

0.001649194434821387

Tolerance#

Since we don’t know the true answer, we can never say that we have reached it. What we can say is that the answer isn’t getting any better.

Programmatically, we say that the error / fractional error has crossed a tolerance.

Define:

The absolute tolerance, \(Tol_a\), is the threshold past which the absolute error is small enough.

The relative tolerance, \(Tol_r\), is the threshold past which the relative error is small enough.

Pseudo code concept#

Run an algorithm for a given parameter
loop:
  reduce parameter
  run algorithm
  Calculate error and relative error
  Exit when tolerance is met

Example: Lets explore \(E_a\) and \(\epsilon_a\) as a function of \(\Delta x\):#

# prompt: Plot E_a and epsilon_a vs delta_x for decending values of delta_x to 1e-10 on a log-log with markers

import matplotlib.pyplot as plt
import numpy as np

delta_x = np.logspace(0,-10,11)
E_a = np.zeros(delta_x.size)
epsilon_a = np.zeros(delta_x.size)

for i, dx in enumerate(delta_x):
  E_a[i] = approx(dx/10) - approx(dx)
  epsilon_a[i] = E_a[i]/approx(dx/10)

plt.loglog(delta_x, E_a, marker='o', label='$E_a$')
plt.loglog(delta_x, epsilon_a, marker='s', label='$\epsilon_a$')
plt.xlabel('$\Delta x$')
plt.ylabel('Error')
plt.legend()
plt.show()
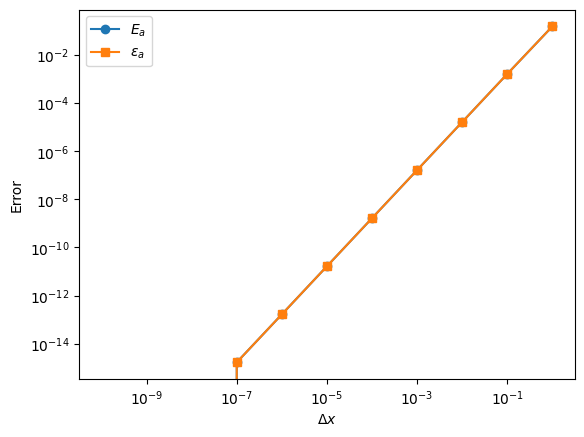
../../_images/0a4eb3056607647db0ddb80a42b68c24bfe9ce797a007bd303afa18f93662d33.png

Note:

  • The two errors overlap. Why?

  • The plot is a straight line. What does this mean?

  • There is a precipitous drop-off at \(10^{-7}\). What is that?

THESE QUESTIONS AND MORE IN THE NEXT EXCITING EPISODE OF NUMERICAL METHODS FOR ENGINEERING!