Polyfit

Let’s return to our polynomial fitting armed with our new tool, and use it to separate the order of the polynomial from the number of data points.

An \(n\) th degree polynomial,

\[ y(x) = a_n x^n + a_{n-1} x^{n-1} \dots a_2 x^2 + a_1 x +a_0\]

can be applied to \(m\) data points,

\(y(x_i) = a_n x_i^n + a_{n-1} x_i^{n-1} \dots a_2 x_i^2 + a_1 x_i +a_0 = y_i\)

to generate an \(m \times n\) matrix, multiplied by an \(n\) vector of polynomial coefficients to equal an \(m\) vector of data:

\[\begin{split} \begin{bmatrix} 1 & x_1 & x_1^2 & \cdots & x_1^n \\ 1 & x_2 & x_2^2 & \cdots & x_2^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_m & x_m^2 & \cdots & x_m^n \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_m \end{bmatrix} \end{split}\]

Example: Determine the coefficients of a cubic polynomial

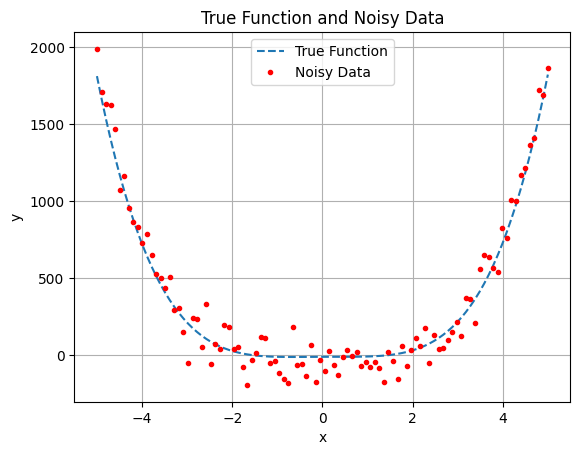
# prompt: generate 100 samples of the function 3x^4-2x^2+x-9 with +-100 noise. Plot the true curve with dashed lines and the data with small points in red.

import matplotlib.pyplot as plt
import numpy as np

# Generate x values
x = np.linspace(-5, 5, 100)

# Define the true function
def true_function(x):
  return 3 * x**4 - 2 * x**2 + x - 9

# Calculate the true y values
y_true = true_function(x)

# Generate noisy data
np.random.seed(0)  # For reproducibility
noise = np.random.normal(0, 100, 100)
x_data = np.linspace(-5, 5, 100)
y_data = true_function(x_data) + noise

# Plot the true curve and the data
plt.plot(x, y_true, '--', label='True Function')
plt.plot(x_data, y_data, 'ro', markersize=3, label='Noisy Data')

plt.xlabel('x')
plt.ylabel('y')
plt.title('True Function and Noisy Data')
plt.legend()
plt.grid(True)
plt.show()

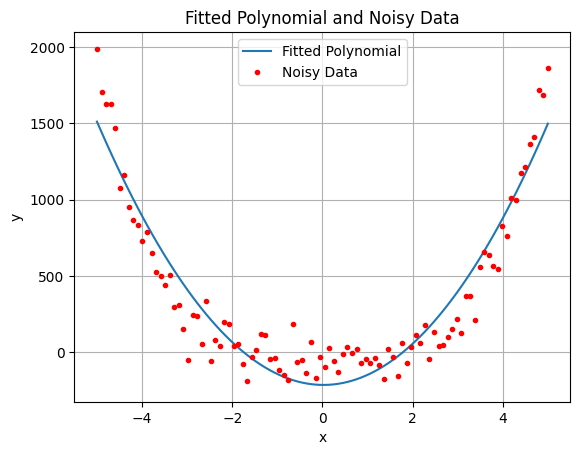
# prompt: Generate the vermonde matrix for a cubic polynomial, invert it using pinv and the y data to find the coefficients of the polynomial and then plot it along with the data

import matplotlib.pyplot as plt
import numpy as np
# Generate the Vandermonde matrix for a cubic polynomial
n = 3  # Degree of the polynomial
X = np.vander(x_data, n + 1)

# Calculate the coefficients using the pseudoinverse
coefficients = np.linalg.pinv(X) @ y_data

coeffs = np.polyfit(x_data, y_data, 3)
print('Coefficients calculated manually', coefficients, '\n')
print('Coefficients calculated with polyfit', coeffs)

# Generate y values for the fitted polynomial
fitted_polynomial = np.poly1d(coeffs)
y_fitted = fitted_polynomial(x)


# Plot the fitted polynomial along with the data
plt.plot(x, y_fitted, label='Fitted Polynomial')
plt.plot(x_data, y_data, 'ro', markersize=3, label='Noisy Data')

plt.xlabel('x')
plt.ylabel('y')
plt.title('Fitted Polynomial and Noisy Data')
plt.legend()
plt.grid(True)
plt.show()

[[-1.25000000e+02  2.50000000e+01 -5.00000000e+00  1.00000000e+00]
 [-1.17576257e+02  2.40001020e+01 -4.89898990e+00  1.00000000e+00]
 [-1.10452422e+02  2.30206101e+01 -4.79797980e+00  1.00000000e+00]
 [-1.03622311e+02  2.20615243e+01 -4.69696970e+00  1.00000000e+00]
 [-9.70797404e+01  2.11228446e+01 -4.59595960e+00  1.00000000e+00]
 [-9.08185260e+01  2.02045710e+01 -4.49494949e+00  1.00000000e+00]
 [-8.48324846e+01  1.93067034e+01 -4.39393939e+00  1.00000000e+00]
 [-7.91154325e+01  1.84292419e+01 -4.29292929e+00  1.00000000e+00]
 [-7.36611859e+01  1.75721865e+01 -4.19191919e+00  1.00000000e+00]
 [-6.84635612e+01  1.67355372e+01 -4.09090909e+00  1.00000000e+00]
 [-6.35163748e+01  1.59192939e+01 -3.98989899e+00  1.00000000e+00]
 [-5.88134431e+01  1.51234568e+01 -3.88888889e+00  1.00000000e+00]
 [-5.43485822e+01  1.43480257e+01 -3.78787879e+00  1.00000000e+00]
 [-5.01156087e+01  1.35930007e+01 -3.68686869e+00  1.00000000e+00]
 [-4.61083388e+01  1.28583818e+01 -3.58585859e+00  1.00000000e+00]
 [-4.23205888e+01  1.21441690e+01 -3.48484848e+00  1.00000000e+00]
 [-3.87461751e+01  1.14503622e+01 -3.38383838e+00  1.00000000e+00]
 [-3.53789141e+01  1.07769615e+01 -3.28282828e+00  1.00000000e+00]
 [-3.22126221e+01  1.01239669e+01 -3.18181818e+00  1.00000000e+00]
 [-2.92411154e+01  9.49137843e+00 -3.08080808e+00  1.00000000e+00]
 [-2.64582103e+01  8.87919600e+00 -2.97979798e+00  1.00000000e+00]
 [-2.38577232e+01  8.28741965e+00 -2.87878788e+00  1.00000000e+00]
 [-2.14334705e+01  7.71604938e+00 -2.77777778e+00  1.00000000e+00]
 [-1.91792685e+01  7.16508520e+00 -2.67676768e+00  1.00000000e+00]
 [-1.70889334e+01  6.63452709e+00 -2.57575758e+00  1.00000000e+00]
 [-1.51562817e+01  6.12437506e+00 -2.47474747e+00  1.00000000e+00]
 [-1.33751297e+01  5.63462912e+00 -2.37373737e+00  1.00000000e+00]
 [-1.17392938e+01  5.16528926e+00 -2.27272727e+00  1.00000000e+00]
 [-1.02425902e+01  4.71635547e+00 -2.17171717e+00  1.00000000e+00]
 [-8.87883529e+00  4.28782777e+00 -2.07070707e+00  1.00000000e+00]
 [-7.64184545e+00  3.87970615e+00 -1.96969697e+00  1.00000000e+00]
 [-6.52543700e+00  3.49199061e+00 -1.86868687e+00  1.00000000e+00]
 [-5.52342628e+00  3.12468115e+00 -1.76767677e+00  1.00000000e+00]
 [-4.62962963e+00  2.77777778e+00 -1.66666667e+00  1.00000000e+00]
 [-3.83786338e+00  2.45128048e+00 -1.56565657e+00  1.00000000e+00]
 [-3.14194388e+00  2.14518927e+00 -1.46464646e+00  1.00000000e+00]
 [-2.53568745e+00  1.85950413e+00 -1.36363636e+00  1.00000000e+00]
 [-2.01291045e+00  1.59422508e+00 -1.26262626e+00  1.00000000e+00]
 [-1.56742922e+00  1.34935211e+00 -1.16161616e+00  1.00000000e+00]
 [-1.19306008e+00  1.12488522e+00 -1.06060606e+00  1.00000000e+00]
 [-8.83619379e-01  9.20824406e-01 -9.59595960e-01  1.00000000e+00]
 [-6.32923460e-01  7.37169677e-01 -8.58585859e-01  1.00000000e+00]
 [-4.34788658e-01  5.73921028e-01 -7.57575758e-01  1.00000000e+00]
 [-2.83031313e-01  4.31078461e-01 -6.56565657e-01  1.00000000e+00]
 [-1.71467764e-01  3.08641975e-01 -5.55555556e-01  1.00000000e+00]
 [-9.39143501e-02  2.06611570e-01 -4.54545455e-01  1.00000000e+00]
 [-4.41874103e-02  1.24987246e-01 -3.53535354e-01  1.00000000e+00]
 [-1.61032836e-02  6.37690032e-02 -2.52525253e-01  1.00000000e+00]
 [-3.47830926e-03  2.29568411e-02 -1.51515152e-01  1.00000000e+00]
 [-1.28826269e-04  2.55076013e-03 -5.05050505e-02  1.00000000e+00]
 [ 1.28826269e-04  2.55076013e-03  5.05050505e-02  1.00000000e+00]
 [ 3.47830926e-03  2.29568411e-02  1.51515152e-01  1.00000000e+00]
 [ 1.61032836e-02  6.37690032e-02  2.52525253e-01  1.00000000e+00]
 [ 4.41874103e-02  1.24987246e-01  3.53535354e-01  1.00000000e+00]
 [ 9.39143501e-02  2.06611570e-01  4.54545455e-01  1.00000000e+00]
 [ 1.71467764e-01  3.08641975e-01  5.55555556e-01  1.00000000e+00]
 [ 2.83031313e-01  4.31078461e-01  6.56565657e-01  1.00000000e+00]
 [ 4.34788658e-01  5.73921028e-01  7.57575758e-01  1.00000000e+00]
 [ 6.32923460e-01  7.37169677e-01  8.58585859e-01  1.00000000e+00]
 [ 8.83619379e-01  9.20824406e-01  9.59595960e-01  1.00000000e+00]
 [ 1.19306008e+00  1.12488522e+00  1.06060606e+00  1.00000000e+00]
 [ 1.56742922e+00  1.34935211e+00  1.16161616e+00  1.00000000e+00]
 [ 2.01291045e+00  1.59422508e+00  1.26262626e+00  1.00000000e+00]
 [ 2.53568745e+00  1.85950413e+00  1.36363636e+00  1.00000000e+00]
 [ 3.14194388e+00  2.14518927e+00  1.46464646e+00  1.00000000e+00]
 [ 3.83786338e+00  2.45128048e+00  1.56565657e+00  1.00000000e+00]
 [ 4.62962963e+00  2.77777778e+00  1.66666667e+00  1.00000000e+00]
 [ 5.52342628e+00  3.12468115e+00  1.76767677e+00  1.00000000e+00]
 [ 6.52543700e+00  3.49199061e+00  1.86868687e+00  1.00000000e+00]
 [ 7.64184545e+00  3.87970615e+00  1.96969697e+00  1.00000000e+00]
 [ 8.87883529e+00  4.28782777e+00  2.07070707e+00  1.00000000e+00]
 [ 1.02425902e+01  4.71635547e+00  2.17171717e+00  1.00000000e+00]
 [ 1.17392938e+01  5.16528926e+00  2.27272727e+00  1.00000000e+00]
 [ 1.33751297e+01  5.63462912e+00  2.37373737e+00  1.00000000e+00]
 [ 1.51562817e+01  6.12437506e+00  2.47474747e+00  1.00000000e+00]
 [ 1.70889334e+01  6.63452709e+00  2.57575758e+00  1.00000000e+00]
 [ 1.91792685e+01  7.16508520e+00  2.67676768e+00  1.00000000e+00]
 [ 2.14334705e+01  7.71604938e+00  2.77777778e+00  1.00000000e+00]
 [ 2.38577232e+01  8.28741965e+00  2.87878788e+00  1.00000000e+00]
 [ 2.64582103e+01  8.87919600e+00  2.97979798e+00  1.00000000e+00]
 [ 2.92411154e+01  9.49137843e+00  3.08080808e+00  1.00000000e+00]
 [ 3.22126221e+01  1.01239669e+01  3.18181818e+00  1.00000000e+00]
 [ 3.53789141e+01  1.07769615e+01  3.28282828e+00  1.00000000e+00]
 [ 3.87461751e+01  1.14503622e+01  3.38383838e+00  1.00000000e+00]
 [ 4.23205888e+01  1.21441690e+01  3.48484848e+00  1.00000000e+00]
 [ 4.61083388e+01  1.28583818e+01  3.58585859e+00  1.00000000e+00]
 [ 5.01156087e+01  1.35930007e+01  3.68686869e+00  1.00000000e+00]
 [ 5.43485822e+01  1.43480257e+01  3.78787879e+00  1.00000000e+00]
 [ 5.88134431e+01  1.51234568e+01  3.88888889e+00  1.00000000e+00]
 [ 6.35163748e+01  1.59192939e+01  3.98989899e+00  1.00000000e+00]
 [ 6.84635612e+01  1.67355372e+01  4.09090909e+00  1.00000000e+00]
 [ 7.36611859e+01  1.75721865e+01  4.19191919e+00  1.00000000e+00]
 [ 7.91154325e+01  1.84292419e+01  4.29292929e+00  1.00000000e+00]
 [ 8.48324846e+01  1.93067034e+01  4.39393939e+00  1.00000000e+00]
 [ 9.08185260e+01  2.02045710e+01  4.49494949e+00  1.00000000e+00]
 [ 9.70797404e+01  2.11228446e+01  4.59595960e+00  1.00000000e+00]
 [ 1.03622311e+02  2.20615243e+01  4.69696970e+00  1.00000000e+00]
 [ 1.10452422e+02  2.30206101e+01  4.79797980e+00  1.00000000e+00]
 [ 1.17576257e+02  2.40001020e+01  4.89898990e+00  1.00000000e+00]
 [ 1.25000000e+02  2.50000000e+01  5.00000000e+00  1.00000000e+00]]
Coefficients calculated manually [ 6.28230705e-02  6.87425501e+01 -2.93452380e+00 -2.14197455e+02] 

Coefficients calculated with polyfit [ 6.28230705e-02  6.87425501e+01 -2.93452380e+00 -2.14197455e+02]

Example 2: Find a series of ‘best fit polynomials’

# prompt: parameterize polyfit for degrees 0 to 10, plotting each on the same plot along with the sample data. Output the norm of the residuals for each fit along with the coefficients to 2 decimal places

import matplotlib.pyplot as plt
import numpy as np

# Generate x values
x = np.linspace(-5, 5, 100)

# Define the true function
def true_function(x):
  return 3 * x**4 - 2 * x**2 + x - 9

# Generate noisy data
np.random.seed(0)  # For reproducibility
noise = np.random.normal(0, 100, 100)
x_data = np.linspace(-5, 5, 100)
y_data = true_function(x_data) + noise

# Plot the true curve and the data
plt.plot(x_data, y_data, 'ro', markersize=3, label='Noisy Data')

for degree in range(11):
    coeffs = np.polyfit(x_data, y_data, degree)
    fitted_polynomial = np.poly1d(coeffs)
    y_fitted = fitted_polynomial(x)
    plt.plot(x, y_fitted, label=f'Degree {degree}')
    residuals = y_data - fitted_polynomial(x_data)
    residual_norm = np.linalg.norm(residuals)
    print(f"Degree {degree}: Residual Norm = {residual_norm:.2f}, Coefficients = {[round(c, 2) for c in coeffs]}")

plt.xlabel('x')
plt.ylabel('y')
plt.title('Fitted Polynomials of Varying Degrees')
plt.legend()
plt.grid(True)
plt.show()

Degree 0: Residual Norm = 5515.03, Coefficients = [370.23]
Degree 1: Residual Norm = 5514.73, Coefficients = [-1.97, 370.23]
Degree 2: Residual Norm = 1759.53, Coefficients = [68.74, -1.97, -214.2]
Degree 3: Residual Norm = 1759.49, Coefficients = [0.06, 68.74, -2.93, -214.2]
Degree 4: Residual Norm = 923.52, Coefficients = [3.03, 0.06, 2.62, -2.93, -45.63]
Degree 5: Residual Norm = 917.81, Coefficients = [-0.08, 3.03, 2.38, 2.62, -15.58, -45.63]
Degree 6: Residual Norm = 917.57, Coefficients = [0.01, -0.08, 2.8, 2.38, 4.56, -15.58, -47.98]
Degree 7: Residual Norm = 916.86, Coefficients = [-0.0, 0.01, 0.1, 2.8, 0.23, 4.56, -9.51, -47.98]
Degree 8: Residual Norm = 916.67, Coefficients = [-0.0, -0.0, 0.05, 0.1, 2.15, 0.23, 7.55, -9.51, -50.1]
Degree 9: Residual Norm = 916.49, Coefficients = [0.0, -0.0, -0.02, 0.05, 0.45, 2.15, -2.0, 7.55, -5.65, -50.1]
Degree 10: Residual Norm = 916.28, Coefficients = [0.0, 0.0, -0.01, -0.02, 0.24, 0.45, 0.53, -2.0, 12.3, -5.65, -52.29]

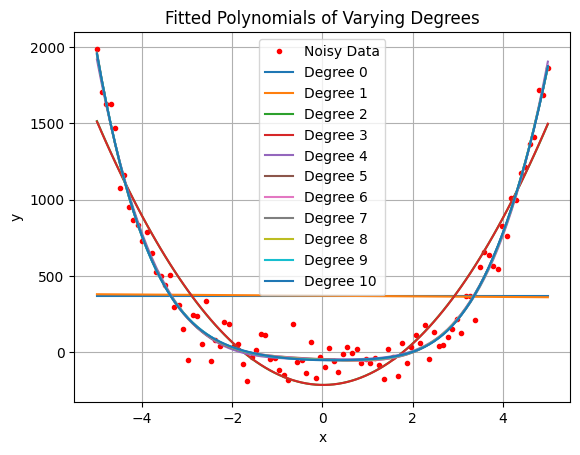
Interesting points: The curve actually is 4th order but because additional terms will always reduce the error, it is not trivial to tell which is the best, best fit!

Example 3: Consider the condition number of the Vermonde matrix for increasing n

# prompt: print the condition number for an increasing series of vermonde matricies on 10 data points

import numpy as np
# Generate x values
x_data = np.linspace(-5, 5, 10)

for degree in range(1, 11):
    # Generate the Vandermonde matrix for a given degree
    X = np.vander(x_data, degree + 1)

    # Calculate the condition number
    condition_number = np.linalg.cond(X)

    print(f"Degree {degree}: Condition Number = {condition_number:.2f}")

Degree 1: Condition Number = 3.19
Degree 2: Condition Number = 20.60
Degree 3: Condition Number = 94.89
Degree 4: Condition Number = 583.63
Degree 5: Condition Number = 2841.25
Degree 6: Condition Number = 17743.56
Degree 7: Condition Number = 95457.72
Degree 8: Condition Number = 648343.57
Degree 9: Condition Number = 5082996.99
Degree 10: Condition Number = 25360712.21

Recall that as the condition number strays from 1, numerical algorithms deteriorate. This is why low-order polynomials are more numerically robust to fit than high order!