GOALS:
Grasp the basic concept of Jacobi, Gauss-Seidel, and Successive Over Relaxation iterative methods
Understand the pros and cons of each method
Experience the benefit of iterative solvers
Jacobi iteration method#
Begin by writing out the linear system in index form:
Extract the \(i\)th row, and solve for the diagonal term:
This makes \(x_i^{k+1}\) consistent with all the other elements.
We can write this in matrix form by pulling appart \(A\) along its diagonal, \(D\), into the upper \(U\) and lower \(L\) matricies:
\(A = L + D + U\)
NB: This is not a matrix decomposition; we are literally just pulling it apart (blank elements are zeros):
The algorithm becomes: $\(\begin{align} D x^{k+1} &= b-[L+U]x^k \\ x^{k+1} &= D^{-1} \big[b-[L+U]x^k\big] \end{align} \)$
Note:
Each new vector uses the entire previous one. We need to store both \(x^k\) and \(x^{k+1}\).
More memory but parallelizes better!
# prompt: Write a code that take a single Jacobi iteration step
import numpy as np
def jacobi_step(A, b, x):
"""Performs a single Jacobi iteration step.
Args:
A: The coefficient matrix.
b: The right-hand side vector.
x: The current solution vector.
Returns:
The updated solution vector.
"""
n = len(x)
x_new = np.zeros_like(x)
for i in range(n):
x_new[i] = (b[i] - np.dot(A[i, :i], x[:i]) - np.dot(A[i, i + 1:], x[i + 1:])) / A[i, i]
return x_new
# Test it!
A = np.array([[4, 1], [1, 3]])
b = np.array([5, 6])
x0 = np.array([0., 0.])
print('Residual for ', x0, ' is ', np.linalg.norm(A@x0-b))
x_new = jacobi_step(A, b, x0)
print('Residual for ', x_new, ' is ', np.linalg.norm(A@x_new-b))
print('The true answer is ', np.linalg.solve(A, b))
Residual for [0. 0.] is 7.810249675906654
Residual for [1.25 2. ] is 2.358495283014151
The true answer is [0.81818182 1.72727273]
Gauss-Seidel#
Gauss-Seidel uses the same concept except that the next guess for \(x_i\) is based on the current version of \(x\). I.e.: If we are moving downwards through the rows, the \(i\)th element is updated based on the updated rows above.
This can again be written in matrix form: $\(\begin{align} A_{ii}x_i^{k+1} + \sum_{j=1}^{i-1} A_{ij} x_j^{k+1} &= b_i-\sum_{j=i+1}^n A_{ij} x_j^k\\ [D + L] x^{k+1} &= b - Ux^{k} \end{align} \)$
Gauss-Seidel is conceptually easier to implement since if we modify \(x\) in place, each \(x_i^{k+1}\) is built from all the other current elements! We can drop the iteration superscript and write (note the arrow for assignment):
Notes:
Each iteration includes the previously updated elements.
We can just store 1 vector and update in-place.
Less memory but doesn’t parallelize as well.
# prompt: Write a code like above that takes a single Gauss-sidel step
import numpy as np
def gauss_seidel_step(A, b, x, omega = 1):
"""Performs a single Gauss-Seidel iteration step.
Args:
A: The coefficient matrix.
b: The right-hand side vector.
x: The current solution vector.
Returns:
The updated solution vector.
"""
n = len(x)
for i in range(n):
x[i] = (b[i] - np.dot(A[i, :i], x[:i]) - np.dot(A[i, i + 1:], x[i + 1:])) / A[i, i]
return x
# Test it!
A = np.array([[4, 1], [1, 3]])
b = np.array([5, 6])
x0 = np.array([0., 0.])
print('Residual for ', x0, ' is ', np.linalg.norm(A@x0-b))
x_new = gauss_seidel_step(A, b, x0.copy())
print('Residual for ', x_new, ' is ', np.linalg.norm(A@x_new-b))
print('The true answer is ', np.linalg.solve(A, b))
Residual for [0. 0.] is 7.810249675906654
Residual for [1.25 1.58333333] is 1.583333333333333
The true answer is [0.81818182 1.72727273]
Successive Over Relaxation (SOR)#
The convergence of Gauss-Sidel can be improved through relaxation: Let’s take a weighted average of the new and old \(x_i^{k+1}\):
Let’s look at three cases:
\(\omega = 1\) the method is exactly Gauss-Seidel (therefore you will usually only find SOR out in the wild)
\(\omega\lt 1\) the method is underrelaxed and will converge / diverge more slowly. Hopefully this will lead to better (albeit slower) convergence…
\(\omega \gt 1\) the method is over relaxed and convergence / divergence will be accelarated!
In general, SOR with a well-chosen \(\omega\) will outperform Gauss-Seidel, but choosing \(\omega\) is not-trivial.
One option: Calculate the difference between successive iterations:
\(\Delta x^k = ||x^{k}-x^{k-1})||\)
After an integer \(p\) more iterations, recalculate:
\(\Delta x^{k+p} =||x^{k+p}-x^{k+p-1}||\)
then the optimal \(\omega\) can be found:
\(\omega_{opt} \approx \frac{2}{1+\sqrt{1+\left[ \frac{\Delta x^{k+p}}{\Delta x^{k}} \right]^p }}\)
# prompt: Write a code that uses the Gauss Seidel function inside a successive over relaxation function to determine step size
import numpy as np
def sor_step(A, b, x):
"""Performs a single SOR iteration step.
Args:
A: The coefficient matrix.
b: The right-hand side vector.
x: The current solution vector.
omega: The relaxation factor.
Returns:
The updated solution vector.
"""
omega = 1.05
n = len(x)
for i in range(n):
x[i] = (1 - omega) * x[i] + (omega / A[i, i]) * (b[i] - np.dot(A[i, :i], x[:i]) - np.dot(A[i, i + 1:], x[i + 1:]))
return x
#Test it!
A = np.array([[4, 1], [1, 3]])
b = np.array([5, 6])
x0 = np.array([0., 0.])
print('Residual for ', x0, ' is ', np.linalg.norm(A@x0-b))
x_new = gauss_seidel_step(A, b, x0.copy())
print('Residual for ', x_new, ' is ', np.linalg.norm(A@x_new-b))
print('The true answer is ', np.linalg.solve(A, b))
Residual for [0. 0.] is 7.810249675906654
Residual for [1.25 1.58333333] is 1.583333333333333
The true answer is [0.81818182 1.72727273]
Summary#
Jacobi, Gauss-Seidel, and SOR are all suitable for large, sparse matricies.
Since the matrix, and therefore the L D U partitions don’t change, terms can be precomputed outside of the iteration loop for computational efficiency.
They generally are more memory efficient and faster but convergence is not guaranteed.
Even with guaranteed convergence, convergence can be slow.
Jacobi
Easily parallelized but slower convergence.
Guaranteed to converge if \(A\) is diagonally dominant
Gauss-Seidel
Faster convergence but doesn’t parallelize well.
Guaranteed to converge if \(A\) is diagonally dominant or symmetric ositive definite.
Successive Over Relaxation
Generalization of Gauss-Seidel (\(\omega = 1\)).
May converge faster.
Success hinges on choice of \(\omega\).
Shares guaranteed convergence of Gauss-Seidel if \(0 \lt \omega \lt 2\).
Let’s code!#
Let’s code in these methods and compare the results. (The python standard libraries don’t have implementaitons).
All the schemes:
Start with a guess, \(A\) matrix and \(b\) vector
Do something to find a new guess (using A and b)
Check how well the guess solves the linear system
Repeats (possibly updating a parameter first)
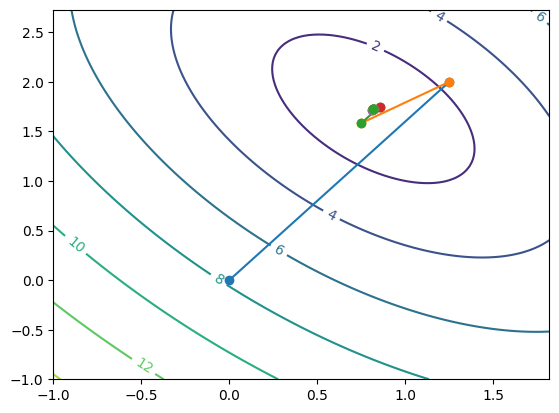
Define a wrapper that implements the above framework, passing a function to do each step. Let’s plot what the system looks like and trace the estimation.
max_iter = 100 # ALWAYS HAVE A FAILSAFE WHEN YOU PLAY WITH INFINITE LOOPS!
tolerance = 1e-6
A = np.array([[4, 1], [1, 3]])
b = np.array([5, 6])
x0 = np.array([0., 0.])
x_true = np.linalg.solve(A, b)
print('The true answer is ', x_true)
# Utility function to autoscale the plot limits to include x0 and x_true
def calculate_box_limits(point1, point2, padding=1.0):
# Extract coordinates
x1, y1 = point1
x2, y2 = point2
# Calculate min and max coordinates with padding
min_x = min(x1, x2) - padding
max_x = max(x1, x2) + padding
min_y = min(y1, y2) - padding
max_y = max(y1, y2) + padding
return (min_x, max_x, min_y, max_y)
xb, xe, yb, ye = calculate_box_limits(x0, x_true)
# Plot the linear system
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x = np.linspace(xb, xe, 100)
y = np.linspace(yb, ye, 100)
X, Y = np.meshgrid(x, y)
V = np.stack((X,Y),-1)
Z = np.linalg.norm(np.matmul(V,A.T)-b, axis = -1)
fig, ax = plt.subplots()
CS = ax.contour(X, Y, Z)
ax.clabel(CS, inline=True, fontsize=10)
method = jacobi_step
#method = gauss_seidel_step
#method = sor_step
for i in range(max_iter):
x_new = method(A, b, x0.copy())
R = np.linalg.norm(A@x_new-b)
print('Iteration ', i, ' determined ', x_new, 'with residual', R)
plt.plot([x0[0], x_new[0]], [x0[1], x_new[1]], '-o')
if np.linalg.norm(R) < tolerance:
print('Converged after, ', i, ' iterations to: ', x_new)
break
x0 = x_new.copy()
The true answer is [0.81818182 1.72727273]
Iteration 0 determined [1.25 2. ] with residual 2.358495283014151
Iteration 1 determined [0.75 1.58333333] with residual 0.650854139658888
Iteration 2 determined [0.85416667 1.75 ] with residual 0.19654127358451298
Iteration 3 determined [0.8125 1.71527778] with residual 0.05423784497157428
Iteration 4 determined [0.82118056 1.72916667] with residual 0.016378439465376277
Iteration 5 determined [0.81770833 1.72627315] with residual 0.004519820414298246
Iteration 6 determined [0.81843171 1.72743056] with residual 0.0013648699554481016
Iteration 7 determined [0.81814236 1.72718943] with residual 0.00037665170119081915
Iteration 8 determined [0.81820264 1.72728588] with residual 0.00011373916295438507
Iteration 9 determined [0.81817853 1.72726579] with residual 3.1387641766271184e-05
Iteration 10 determined [0.81818355 1.72727382] with residual 9.47826357947717e-06
Iteration 11 determined [0.81818154 1.72727215] with residual 2.6156368136569228e-06
Iteration 12 determined [0.81818196 1.72727282] with residual 7.898552987055788e-07
Converged after, 12 iterations to: [0.81818196 1.72727282]
Example: Iteratively solve a large matrix#
# prompt: Form a large, sparse linear system with a diagonally dominant random matrix
import numpy as np
def create_diagonally_dominant_matrix(n):
"""Creates a diagonally dominant random matrix.
Args:
n: The size of the matrix.
Returns:
A diagonally dominant random matrix.
"""
A = np.random.rand(n, n)
for i in range(n):
A[i, i] = np.sum(np.abs(A[i, :])) + np.random.rand() # Ensure diagonal dominance
return A
# put this into a function for convenience
def iter_solve(A, b, method):
x0 = np.zeros(b.shape[0])
max_iter = 1000
tolerance = 1e-6
for i in range(max_iter):
x_new = method(A, b, x0.copy())
R = np.linalg.norm(A@x_new-b)
#print('Iteration ', i, ' determined ', x_new, 'with residual', R)
if np.linalg.norm(R) < tolerance:
print('Converged after, ', i, ' iterations.')
break
x0 = x_new.copy()
n=4#
n = 4 # Size of the matrix
A = create_diagonally_dominant_matrix(n)
b = np.random.rand(n) # Create a random right-hand side vector
print('LU')
%timeit -n1 -r1 np.linalg.solve(A, b)
print('\nJacobi')
%timeit -n1 -r1 iter_solve(A, b, jacobi_step)
print('\nGauss-Seidel')
%timeit -n1 -r1 iter_solve(A, b, gauss_seidel_step)
print('\nSOR')
%timeit -n1 -r1 iter_solve(A, b, sor_step)
LU
43.1 μs ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
Jacobi
Converged after, 27 iterations.
849 μs ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
Gauss-Seidel
Converged after, 8 iterations.
232 μs ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
SOR
Converged after, 9 iterations.
265 μs ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
n = 100#
n = 100 # Size of the matrix
A = create_diagonally_dominant_matrix(n)
b = np.random.rand(n) # Create a random right-hand side vector
print('LU')
%timeit -n1 -r1 np.linalg.solve(A, b)
print('\nJacobi')
%timeit -n1 -r1 iter_solve(A, b, jacobi_step)
print('\nGauss-Seidel')
%timeit -n1 -r1 iter_solve(A, b, gauss_seidel_step)
print('\nSOR')
%timeit -n1 -r1 iter_solve(A, b, sor_step)
LU
107 μs ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
Jacobi
Converged after, 776 iterations.
204 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
Gauss-Seidel
Converged after, 10 iterations.
3.15 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
SOR
Converged after, 11 iterations.
3.53 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
n = 1000#
n = 1000 # Size of the matrix
A = create_diagonally_dominant_matrix(n)
b = np.random.rand(n) # Create a random right-hand side vector
print('LU')
%timeit -n1 -r1 np.linalg.solve(A, b)
#print('\nJacobi')
#%timeit -n1 -r1 iter_solve(A, b, jacobi_step)
print('\nGauss-Seidel')
%timeit -n1 -r1 iter_solve(A, b, gauss_seidel_step)
#print('\nSOR')
#%timeit -n1 -r1 iter_solve(A, b, sor_step)
LU
20.5 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
Gauss-Seidel
Converged after, 10 iterations.
47.4 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
n = 3000#
n = 3000 # Size of the matrix
A = create_diagonally_dominant_matrix(n)
b = np.random.rand(n) # Create a random right-hand side vector
print('LU')
%timeit -n1 -r1 np.linalg.solve(A, b)
#print('\nJacobi')
#%timeit -n1 -r1 iter_solve(A, b, jacobi_step)
print('\nGauss-Seidel')
%timeit -n1 -r1 iter_solve(A, b, gauss_seidel_step)
#print('\nSOR')
#%timeit -n1 -r1 iter_solve(A, b, sor_step)
LU
426 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
Gauss-Seidel
Converged after, 10 iterations.
182 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
n = 5000#
HERE WE GO! Remember, this is a terrible implementation of GS! Numpy with loops is going to be slow!
n = 5000 # Size of the matrix
A = create_diagonally_dominant_matrix(n)
b = np.random.rand(n) # Create a random right-hand side vector
print('LU')
%timeit -n1 -r1 np.linalg.solve(A, b)
#print('\nJacobi')
#%timeit -n1 -r1 iter_solve(A, b, jacobi_step)
print('\nGauss-Seidel')
%timeit -n1 -r1 iter_solve(A, b, gauss_seidel_step)
#print('\nSOR')
#%timeit -n1 -r1 iter_solve(A, b, sor_step)
LU
1.88 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
Gauss-Seidel
Converged after, 11 iterations.
401 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)


