Nomenclature#
Capital letters are Matricies: \(A\)
Vectors have arrows above: \(\vec{x}\)
Scalars are lower case: \(\alpha\)
Superscripts generally denote iteration number: \(\vec{x}^k\).
Conjugate gradient (CG)#
Conjugate gradient method is a standard tool for solving symmetric positive definite systems.
Consider a quadratic surface, defined by:
\(f(\vec{x}^k) = \frac{1}{2} \vec{x}^T A \vec{x} -\vec{b}^T \vec{x}\).
This surface has a minimum at:
\begin{align} \frac{d f}{ d x} = \vec{0} &= A \vec{x}-\vec{b} \ \vec{0} &= \vec{r} \end{align}
Where \(\vec{r}=A \vec{x}-\vec{b} \) is the residual. Minimizing \(f\) is equivilant to solving \(A\vec{x} = \vec{b}\) which is equiviliant to finding \(\vec{r}=\vec{0}\).
For a general guess \(\vec{x}^k\),
\begin{align} A \vec{x}^k-\vec{b} =\vec{r}^k \ne 0 \ \end{align}
The Hessian#
Note: The matrix \(A\) in this case is the hessian, \(H\), of \(f\), which is the matrix made by the mixed second derivatives:
\(H = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}\)
From the rule of mixed second derivatives, we see that the Hessian is symmetric.
The Hessian is positive definite if \(\vec{x}^T H \vec{x} > 0\) for all \(\vec{x}\). In this case the quadratic surface \(f\) is convex (opening upwards). For a 1D case, this means you have a positive second derivative.
For comparison, the other common function with second derivatives is the Laplacian, which is a scalar sum of the diagonal elements of H: \(\Delta f = \nabla^2 f = \frac{\partial^2 f}{\partial x_1^2} + \frac{\partial^2 f}{\partial x_2^2} + \frac{\partial^2 f}{\partial x_3^2} ... \)
Since \(A\) is symmetric, you could form a surface \(f\) which has an extrenum at the solution of the system. These problems are generally called saddle point problem.
Since \(A\) is symmetric positive definite, the surface is convex quadratic (paraboloid) which has a minimum at the solution of the linear system.
##The algorithm
Starting at \(\vec{x}^k\), we will choose step direction \(\vec{s}^k\), and step length \(\alpha^k\) to reach our next guess \(\vec{x}^{k+1}\):
\(\vec{x}^{k+1} = \vec{x}^k + \alpha^k \vec{s}^k\)
Choose the step length#
An obvious choice for \(\alpha^k\) is whatever minimizes \(f(\vec{x}^{k+1})\)!
\(f(\vec{x}+\alpha^k \vec{s}^k) = \frac{1}{2} [\vec{x}+\alpha^k \vec{s}^k]^T A [\vec{x}+\alpha^k \vec{s}^k] -\vec{b}^T [\vec{x}+\alpha^k \vec{s}^k]\).
The minimum is found when:
\begin{align} \frac{\partial f}{\partial \alpha^k} = 0 &= {\vec{s}^k}^T A [\vec{x}+\alpha^k \vec{s}^k] -\vec{b}^T \vec{s}^k\ &= {\vec{s}^k}^T A \vec{x}^k+ {\vec{s}^k}^T A \alpha^k \vec{s}^k -{\vec{s}^k}^T \vec{b} \ &= {\vec{s}^k}^T [A \vec{x}^k-\vec{b}] + \alpha^k {\vec{s}^k}^T A \vec{s}^k \ \alpha_k &= \frac{{\vec{s}^k}^T \vec{r}^k}{{\vec{s}^k}^T A \vec{s}^k} \end{align}
So given a step direction \(\vec{s}^k\) we can take an optimal step length \(\alpha_k\) which is determined by the current residual \(\vec{r}^k\).
Choose the step direction: Steepest descent#
The magic of these methods comes from the choice of step direction.
How do we go about choosing \(\vec{s}^k\)?
The intuitive answer is the negative gradient of \(f(x^k)\), which is simply,
\(s^k = -\nabla f = -\frac{d f}{d\vec{x}} = -\vec{r}^k\)
The optimal step size is therefore,
\(\alpha_k=\frac{{\vec{r}^k}^T \vec{r}^k}{{\vec{r}^k}^T A \vec{r}^k}\)
Now we take the step to form \(\vec{x}^{k+1}\) and repeat the process until your choice of tolerance on the residual (or \(\vec{x}^k\)!) is met.
Let’s code it!
# Copy the surface plotter from the last lecture:
import numpy as np
import matplotlib.pyplot as plt
def plot_surface(A, b, x0, x_true):
# Utility function to autoscale the plot limits to include x0 and x_true
def calculate_box_limits(point1, point2, padding=.5):
# Extract coordinates
x1, y1 = point1
x2, y2 = point2
# Calculate min and max coordinates with padding
min_x = min(x1, x2) - padding
max_x = max(x1, x2) + padding
min_y = min(y1, y2) - padding
max_y = max(y1, y2) + padding
return (min_x, max_x, min_y, max_y)
xb, xe, yb, ye = calculate_box_limits(x0, x_true)
# Plot the linear system
x = np.linspace(xb, xe, 100)
y = np.linspace(yb, ye, 100)
X, Y = np.meshgrid(x, y)
V = np.stack((X,Y),-1)
Z = 0.5 * (A[0, 0] * X**2 + A[1, 1] * Y**2 + 2 * A[0, 1] * X * Y) - (b[0] * X + b[1] * Y)
fig, ax = plt.subplots()
CS = ax.contour(X, Y, Z, levels = 15)
ax.set_xlim([xb, xe]) # Set x-axis limits
ax.set_ylim([yb, ye]) # Set y-axis limits
ax.clabel(CS, inline=True, fontsize=10)
return fig
# prompt: write a function to solve a linear system using the method of steepest descent
import numpy as np
def steepest_descent(A, b, x0, tol=1e-6, max_iter=100):
"""
Solves a linear system Ax = b using the method of steepest descent.
Args:
A: The coefficient matrix (must be symmetric positive definite).
b: The right-hand side vector.
x0: The initial guess for the solution.
tol: The tolerance for the residual.
max_iter: The maximum number of iterations.
Returns:
x: The approximate solution.
residuals: A list of the residuals at each iteration.
"""
x = x0
iterations = [x]
for i in range(max_iter):
r = A @ x - b
if np.linalg.norm(r) < tol:
break
alpha = np.dot(r, r) / np.dot(r, A @ r)
x = x - alpha * r
print('Iteration ', i, ' : ',x)
iterations.append(np.copy(x))
return x, iterations
A = np.array([[4, 1], [1, 3]])
b = np.array([5, 6])
x0 = np.array([0., 0.])
x_true = np.linalg.solve(A, b)
print('The true answer is ', x_true)
fig = plot_surface(A, b, x0, x_true)
_, iterations = steepest_descent(A, b, x0)
iterations = np.array(iterations)
plt.plot(iterations[:, 0], iterations[:, 1], marker='', linestyle='-')
plt.grid(True)
plt.show()
The true answer is [0.81818182 1.72727273]
Iteration 0 : [1.1380597 1.36567164]
Iteration 1 : [0.78590538 1.65913358]
Iteration 2 : [0.83080067 1.71300793]
Iteration 3 : [0.81690855 1.72458471]
Iteration 4 : [0.81867962 1.72671 ]
Iteration 5 : [0.81813159 1.72716669]
Iteration 6 : [0.81820146 1.72725053]
Iteration 7 : [0.81817984 1.72726854]
Iteration 8 : [0.81818259 1.72727185]
Iteration 9 : [0.81818174 1.72727256]
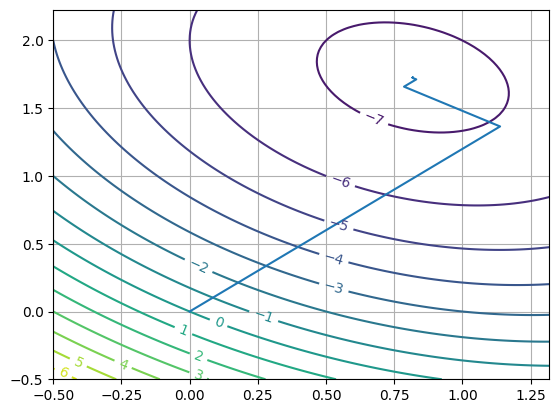
The approach results in the final \(\vec{x}^{approx}\) (eg: after 9 iterations) being formed as:
\(\vec{x}^{9} = \vec{x}^0 + \alpha^1 \vec{s}^1 + \alpha^2 \vec{s}^2 + \alpha^3 \vec{s}^3 ...\)
Let’s consider this for a minute. We are assembling the vector that moves from \(\vec{x}^0\) to \(~\vec{x}^9\), as a series of 9 steps in directions \(\vec{s}^k\) with magnitude \(\alpha^k\).
-> What does this expression remind you of?
This path is inefficient because you end up with zig-zagging where one step undoes some of the others which is inefficient.
-> How do we ensure the next step doesn’t undo the previous step?
Choose the step direction: Conjugate gradient#
The problem is that certain steps undo the effect of the previous step(s). We can instead choose successive step directions to not undo each other, by requiring the next step be conjugate to each other.
This means we must base the \(\vec{s}^{k+1}\) step on the \(\vec{s}^{k}\) step and the gradient descent (which we just saw was \(\vec{r}^k\)).
\(\vec{s}^{k+1} = \vec{r}^{k+1}+\beta^k \vec{s}^k\)
and require that \(\vec{s}^{k+1}\) and \(\vec{s}^k\) are conjugate to each other in \(A\):
\({\vec{s}^{k+1}}^T A \vec{s}^k = 0\)
This does not mean that \(\vec{s}^{k+1}\) and \(\vec{s}^k\) are orthogonal; rather vectors \(\vec{s}^{k+1}\) and \(A \vec{s}^k\) (or equivilantly \(A \vec{s}^{k+1}\) and \(\vec{s}^k\)) are orthogonal.
We can then solve,
\begin{align} [\vec{r}^{k+1}+\beta^k \vec{s}^k]^T A \vec{s}^k &= 0\ \beta^k &= -\frac{\vec{r}^{k+1} A \vec{s}^k}{{\vec{s}^k}^T A \vec{s}^k} \end{align}
and so we find the next step direction,
\(s^{k+1} = r^{k+1} -\frac{r^{k+1} A s^k}{{s^k}^T A s^k} s^k\).
The step length \(\alpha_k\) is determined exactly as before.
Actually, we are going to make the new step direction conjugate to all the previous directions, so we have to say:
\(\vec{s}^{k+1} = \vec{r}^{k+1} - \sum_{i<k}\frac{\vec{r}^{k+1} A \vec{s}^k}{{\vec{s}^k}^T A \vec{s}^k} \vec{s}^k\).
A = np.array([[4, 1], [1, 3]])
b = np.array([5, 6])
x0 = np.array([0., 0.])
x_true = np.linalg.solve(A, b)
print('The true answer is ', x_true)
The true answer is [0.81818182 1.72727273]
# prompt: call a cg solve on this system, but build a list of the iterations
from scipy.sparse.linalg import cg
import numpy as np
iterations = [x0]
print(x0)
def print_iteration_and_save(xk):
iterations.append(np.copy(xk))
print(xk)
solution, info = cg(A, b, x0=x0, callback=print_iteration_and_save)
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[5], line 2
1 # prompt: call a cg solve on this system, but build a list of the iterations
----> 2 from scipy.sparse.linalg import cg
3 import numpy as np
5 iterations = [x0]
ModuleNotFoundError: No module named 'scipy'
iterations = np.array(iterations)
fig = plot_surface(A, b, x0, x_true)
# Plot the iterations on a 2D surface
plt.plot(iterations[:, 0], iterations[:, 1], marker='', linestyle='-')
plt.grid(True)
plt.show()

Let’s examine the steps, which we can find as the difference between successive iterations:
s1 = iterations[1,:]-iterations[0,:]
s2 = iterations[2,:]-iterations[1,:]
print(s1,s2)
print(np.dot(s1,s2)) #not zero
print(np.dot(s1,A@s2)) #Zero
print(np.dot(s2,A@s1)) #Zero
[1.1380597 1.36567164] [-0.35215432 0.29346194]
-1.6653345369377348e-16
-0.547722612647829
-0.5477226126478292
Successive steps are conjugate in \(A\) as expected.
Another interesting property is that the residual at each step is orthogonal:
r0 = A@iterations[0,:]-b
r1 = A@iterations[1,:]-b
r2 = A@iterations[2,:]-b
print(r0.dot(r1))
print(r1.dot(r2))
0.0
-2.7755575615628914e-16
which helps with computational efficiency.
Analysis#
Beginning at \(\vec{x}^0\), we are tasked with finding \(\vec{x}^{approx}\) through an expansion:
\(\vec{x}^{approx} - \vec{x}^0 = \alpha^1 \vec{s}^1 + \alpha^2 \vec{s}^2 + ...\).
but this is simply vector addition using a set of directions. Our algorithms has generated the directions \(\vec{s}^k\) which form a set of vector bases for:
\(\vec{x}^{approx} - \vec{x}^0\)
and, at the same time, the corresonding components, the \(\alpha^k\).
The method of steepest descent doesn’t enforce all vector bases be orthogonal (or conjugate), resulting in frenetic zig-zagging and more bases than necessary.
The conjugate gradient method enforces conjugacy in the vector bases such that they don’t overlap. Vectors are linearly independent from the matrix-vector products of the others. This algorithm relies on \(A\) being SPD.
Note that these techniques only ever use \(A\) in the context for a matrix-vector product - \(A \vec{x}\). Matrix-vector products are \(O(n^2)\) (for dense matricies, better for sparse) but there is also the storage requirement for \(A\). If we can find a better way to get the vector \(A\vec{x}\) that doesn’t involve (assembling), storing, and multiplying \(A\), we can see improvements. This is the basis of Matrix-free algorithms.
Note the space of the solution vector \(x\) is just its dimension \(n\), and if CG determins linearly independent vectors, it can only find, at most \(n\)! Therefore, CG will find the exact solution in \(n\) iterations (baring roundoff error) which some may take to imply it is a direct method. However, the situation is even better, which qualifies it as an iterative technique! Let’s see what happens with a larger system:
# prompt: Solve a 10x10 random spd linear system with CG
import numpy as np
from scipy.sparse.linalg import cg
n = 8
A_r = np.random.rand(n, n)
A_rand = A_r @ A_r.T # Ensure A is symmetric positive definite
b_rand = np.random.rand(n)
x0_rand = np.zeros(n)
class it_counter(object):
def __init__(self, disp=True):
self._disp = disp
self.niter = 0
def __call__(self, rk=None):
self.niter += 1
if self._disp:
print('iter %3i\trk = %s' % (self.niter, str(rk)))
np.set_printoptions(precision=4)
solution, info = cg(A_rand, b_rand, x0=x0_rand, atol = 1e-6, rtol = 1e-10, callback = it_counter())
print("Solution:", solution)
print("Info:", info)
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[9], line 4
1 # prompt: Solve a 10x10 random spd linear system with CG
3 import numpy as np
----> 4 from scipy.sparse.linalg import cg
6 n = 8
7 A_r = np.random.rand(n, n)
ModuleNotFoundError: No module named 'scipy'
Note that successive iterations are getting closer and closer. Usually, the estimates converge before \(n\) iterations (which is especially useful for large sparse matricies!)
###Restart
Sometimes, the set of \(s^k\) gets too large and round-off error can accumulate. Therefore, some implementation have an integer ‘restart’ parameter which will trigger a restart of the bases after a set number have been generated.
Generalized Minimal Residual Method (GMRES)#
Let’s finally turn our attention towards the general case of \(A\) being a general non-symmetric matrix. Since it is non-symmetric, it can not be a Hessian and there is no quadratic surface associated with it.
We can adapt the same basic method of CG:
Take the residual of the system, \(\vec{r} = A\vec{x}-\vec{b}\) and minimize its Euclidian norm, \(||\vec{r}||\).
Beginning with \(\vec{x}^0\), construct a basis for \(\vec{x}^{approx}-\vec{x}^0\) in \(\vec{s}^k\).
Enforce orthogonality with successive \(\vec{s}^{k}\)
Since each \(\vec{s}^k\) is linearly independent, the method will converge in at most \(n\) iterations, but typically converges much sooner.
A restart may still be necessary to control memory consumption for large systems.
The major difference is that the conjugacy of \(\vec{s}^k\) is not possible since \(A\) is not SPD. Rather, \(\vec{s}^k\) are chosen to be orthogonal which is a more general, but less powerful condition.
from scipy.sparse.linalg import gmres
A = np.array([[4, 1], [1, 3]])
b = np.array([5, 6])
x0 = np.array([0., 0.])
iterations = [x0]
print(x0)
def print_iteration_and_save(xk):
iterations.append(np.copy(xk))
print(xk)
solution, info = gmres(A, b, callback=it_counter(), callback_type = 'legacy') #x
np.linalg.solve(A,b)
print(iterations)
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[10], line 1
----> 1 from scipy.sparse.linalg import gmres
2 A = np.array([[4, 1], [1, 3]])
3 b = np.array([5, 6])
ModuleNotFoundError: No module named 'scipy'
np.set_printoptions(precision=4)
solution, info = gmres(A_rand, b_rand, x0=x0_rand, atol = 1e-6, rtol = 1e-10, callback = it_counter(), callback_type='legacy')
print("Solution:", solution)
print("Info:", info)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[11], line 3
1 np.set_printoptions(precision=4)
----> 3 solution, info = gmres(A_rand, b_rand, x0=x0_rand, atol = 1e-6, rtol = 1e-10, callback = it_counter(), callback_type='legacy')
4 print("Solution:", solution)
5 print("Info:", info)
NameError: name 'gmres' is not defined

