Polynomial interpolation#
Polynomial interpolation is a straightforward approach to interpolation.
Three methods to obtain polynomials are established here. For a given set of data, they all must result in the same polynomial. The difference is the means by which they are achieved, which translates to the ways that they are used.
Lagrange Polynomial Interpolation#
Legendre polynomial interpolation constructs the Legendre polynomial as, $\( y(x) = \sum_{i = 1}^n y_i P_i(x) \)$
which is a weighted sum of the Lagrange basis polynomials, \(P_i(x)\),
N.B.: \(\prod\) means the product of, like \(\sum\) means the sum of.
Lagrange basis polynomials#
By construction,
\(P_i(x_j) = 1\) when \(i = j\)
\(P_i(x_j) = 0\) when \(i \ne j\).
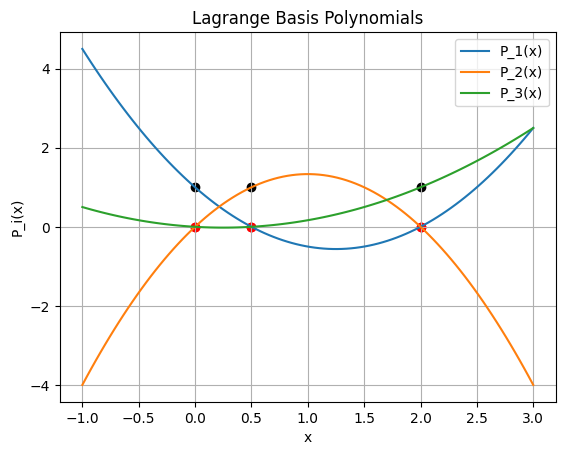
Example: Find and plot the Lagrange basis polynomials#
Use the data: x = [0, .5, 2] y = [1, 3, 2]
\begin{eqnarray} P_1(x) &=& \frac{(x - x_2)(x - x_3)}{(x_1-x_2)(x_1-x_3)} = \frac{(x - 1)(x - 2)}{(0-1)(0-2)} = \frac{1}{2}(x^2 - 3x + 2),\ P_2(x) &=& \frac{(x - x_1)(x - x_3)}{(x_2-x_1)(x_2-x_3)} = \frac{(x - 0)(x - 2)}{(1-0)(1-2)} = -x^2 + 2x,\ P_3(x) &=& \frac{(x - x_1)(x - x_2)}{(x_3-x_1)(x_3-x_2)} = \frac{(x - 0)(x - 1)}{(2-0)(2-1)} = \frac{1}{2}(x^2 - x). \end{eqnarray}
Plot each polynomial and verify the property that \(P_i(x_j) = 1\) when \(i = j\) and \(P_i(x_j) = 0\) when \(i \ne j\).
# prompt: show me the legendre basis polynomials for the data aove using the numpy.polynomial.legendre Legendre
import numpy as np
import matplotlib.pyplot as plt
from numpy.polynomial import legendre
# Data points
x = [0, .5, 2]
y = [1, 3, 2]
# Calculate the Lagrange basis polynomials
n = len(x)
P = []
for i in range(n):
numerator = 1
denominator = 1
for j in range(n):
if i != j:
numerator = np.polymul(numerator, np.poly1d([1, -x[j]]))
denominator = denominator * (x[i] - x[j])
P.append(np.poly1d(np.polydiv(numerator, denominator)[0]))
# Plot the Lagrange basis polynomials
x_plot = np.linspace(-1, 3, 100)
for i in range(n):
y_plot = P[i](x_plot)
plt.plot(x_plot, y_plot, label=f'P_{i+1}(x)')
plt.scatter(x, [1] * len(x), color='black')
plt.scatter(x, [0] * len(x), color='red')
plt.scatter(x, [0] * len(x), color='red')
plt.xlabel('x')
plt.ylabel('P_i(x)')
plt.title('Lagrange Basis Polynomials')
plt.legend()
plt.grid(True)
plt.show()
Assembling the polynomial#
Since \(P_{i\ne j}=0\), and \(P_{i = j}=1\), it is trivial to see that for \( y(x) = \sum_{i = 1}^n \omega_i P_i(x) \), the coefficients are simply:
# prompt: Plot the legendre polynomial from the basis above
import matplotlib.pyplot as plt
import numpy as np
# Construct the Lagrange polynomial
L = np.poly1d(0)
for i in range(n):
L = L + y[i] * P[i]
# Plot the Lagrange polynomial
y_plot = L(x_plot)
plt.plot(x_plot, y_plot, label='L(x)')
plt.scatter(x, y, color='red', label='Data points')
plt.xlabel('x')
plt.ylabel('L(x)')
plt.title('Lagrange Polynomial Interpolation')
plt.legend()
plt.grid(True)
plt.show()
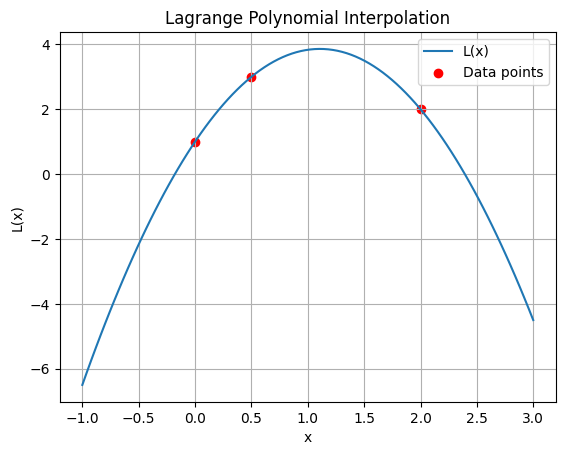
Analysis#
We can observe some notes:
For \(n\) data points we necessarily produce a unique polynominal that crosses each one.
If we have two measurements at the same input, \(x_i = x_j\), \(P_i =\sim \frac{1}{0}\) which is undefined unless \(x_i=x_j\) and \(y_i=y_j\) in which case the data pair is redundant and can be removed.
Each evalulation of \(P(x)\) involves \(n-1\) products, and \(L(x)\) is the sum of \(n\) bases, therefore evaluation is \(O(n^2)\)
Adding new data means restarting the compuation.
# prompt: Use sympy to fit a lagrange polynomial to the data above (with some extra points)
import sympy as sp
x = [0, 1, 2, 3, 4]
y = [1, 3, 2, 5, 7]
n = len(x)
x_sym = sp.Symbol('x')
L = 0
for i in range(n):
term = y[i]
for j in range(n):
if i != j:
term *= (x_sym - x[j]) / (x[i] - x[j])
L += term
print(L)
print('which is an ugly way of writing out:')
print(L.simplify())
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[3], line 3
1 # prompt: Use sympy to fit a lagrange polynomial to the data above (with some extra points)
----> 3 import sympy as sp
5 x = [0, 1, 2, 3, 4]
6 y = [1, 3, 2, 5, 7]
ModuleNotFoundError: No module named 'sympy'
Error#
It can be shown that the error in the interpolation is,
where \(\xi\) is in the interval \((x_0, x_n)\).
Since for \(n\) datapoints there is a unique polynomial of degree \(n-1\), which can be expressed as a Lagrange polynomial, this analysis is universal to all polynomial interpolations!. The main takeaway is that:
The further a data point is from \(x\), the more it contributes to the error.
##Barycentric Lagrange Interpolation
Let’s try to improve the performance of Lagrange Interpolation. Let:
\( \Omega(x) = \prod_{j = 1}^n [x - x_j] \)
and the barycentric weights, \(w_i\):
and write:
and factor the \(\Omega\) out of the sum:
which is \(O(n)\) for evaluation. Calculation of \(w_i\) can be formulated recursively, such that each \(w_i\) takes \(O(n)\) and the full takes \(O(n^2)\) with updates n.
NB: The weights depend only on \(x_i\), not \(y_i\) - this means if we are measuring multiple functions on the same spacing, we can reuse the weights, leading to substantial computaitonal savings.
The benefit being that the calucation of the \(\omega_i\), \(O(n^2)\) is precomputed.
Barycentric formula#
We can write one more form which is commonly implemented. Let’s add one more piece of data:
then we divide the previous function and write:
where we have cancelled \(\Omega\)! Besides elegance, his avoids an issue when evaluating \(x\rightarrow x_i\) where roundoff can cause subtractive cancellation. Since the term appears in the numerator and denominator this cancels out!
Newton’s divided difference method#
Newton’s polynomial interpolation has the form:
which has the advantage of \(O(n)\) evaluations due to recursion and nested multiplication. E.g. for 4 terms,
Newton’s method is also known as the divided differences
This was the algorithm was used to calculate function tables like logarithms and trignometry functions. It was then the basis for the difference engine, an early mechanical calculator.
Let’s pick a data point to start at. Say \(y(x_0) = a_0 = y_0\), $\(a_0 = y_0\)$
Add the next data point: \(y(x_1) = a_0 + a_1(x_1-x_0) = y_1\), or:
Now, insert data point \((x_2, y_2)\),
and similarly,
Notice the recurrsion and the division of the differences.
Let’s generalize this. Define the two-argument function:
and the ternary recursively:
The \(n-nary\) function is:
We can visualize this is in a tableau: $\( \begin{array}{cccccc} x_0 & y_0 \\ & & y[x_1,x_0] \\ x_1 & y_1 & & y[x_2, x_1,x_0]\\ & & y[x_2,x_1] & & y[x_3, x_2, x_1,x_0]\\ x_2 & y_2 & & y[x_3, x_2,x_1] & & y[x_4, x_3, x_2, x_1,x_0]\\ & & y[x_3,x_2] & & y[x_4, x_3, x_2, x_1]\\ x_3 & y_3 & & y[x_4, x_3,x_2]\\ & & y[x_4,x_3] \\ x_4 & y_4 \end{array} \)$
where element is the difference of the two to the left. Alternately, it is sometimes written in the form,
Note that the diagonal is the coefficients that we need, i.e. \(a_0, a_1, a_2, a_3, a_4\) for the polynomial.
Direct solution#
Lastly, there is a direct solution method that only became really poractical with the advent of modern computing since it focusses on linear systes:
Consider fitting a function
since
\(y(x_i) = a_n x_i^n + a_{n-1} x_i^{n-1} \dots a_2 x_i^2 + a_1 x_i +a_0 = y_i\)
we can write out in matrix form,
where the matrix of coefficients is called a Vandermonde matrix. This system can be solved for \(a_i\) with a dense linear solver. The issue with this method is that the system is notoriously ill-conditioned and roundoff error accumulates rapidly for large \(n\).
#Example: Interpolate our toy problem
Let us know examine our toy problem. Since all the polynomial interpolation functions generate the same unique polynomial, any will suffice:
# prompt: Interpolate the data in x_d and y_d using numpy Legendre, and plot along with the original curve from -5.5 to 5.5
import matplotlib.pyplot as plt
import numpy as np
# Interpolate using numpy Legendre
coefficients = legendre.legfit(x_d, y_d, len(x_d) - 1)
legendre_polynomial = legendre.Legendre(coefficients)
# Create x values for plotting the interpolated polynomial
x_interp = np.linspace(-5.5, 5.5, 200)
y_interp = legendre_polynomial(x_interp)
# Plot the original curve, sampled points, and interpolated polynomial
plt.plot(x_toy, y_toy, label='exp(-(x/2)^2)')
plt.scatter(x_d, y_d, color='red', label='Sampled points')
plt.plot(x_interp, y_interp, label='Legendre Interpolation')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Function, Sampled Points, and Legendre Interpolation')
plt.grid(True)
plt.show()
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[4], line 6
4 import numpy as np
5 # Interpolate using numpy Legendre
----> 6 coefficients = legendre.legfit(x_d, y_d, len(x_d) - 1)
7 legendre_polynomial = legendre.Legendre(coefficients)
9 # Create x values for plotting the interpolated polynomial
NameError: name 'x_d' is not defined
YIKES!
This is an example of Runge’s phenomenon: That even for a seeminlgly ideal case of equalspaced samples, higher order polynomials can show huge oscillations between samples!
The order that the datapoints are added is arbitrary but will result in a different tableau (with the same diagonal).
We can build this matrix / tableau diagonal-by-diagonal which means adding new data points doesn’t require recalculation of the others.
Each new diagonal (datapoint) takes \(O(n)\) so assembly of the tableau takes \(~O(n^2)\).
Evaluation of f(x) takes \(O(n)\)
These coefficients are independant of \(x\)
Summary#
Let’s recap and generalize:
For any \(n\) points there is a polynomial that fits it, but because of Runge’s phenomenon you don’t want to use that!
Piecewise polynomials are stiffer and avoids Runge’s phenomenon, but smoothness causes issues for N-D So what do we do? Standard pacakges offer simplistic but pragmatic interpolators (optimized for either rectangular or irregular grids) :
Nearest ND interpolator: Find the nearest data point and use that.
Linear ND interpolators: For each input, a triangulation finds the nearest data points and a linear barycentric Lagrange interpolation is performed.
Neither of these are completely satisfactory, so we will have to respost to more advanced methods.

